MAKE A MEME
View Large Image
| View Original: | Delta sigma dithering 1st order err vs frq.svg (753x482) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
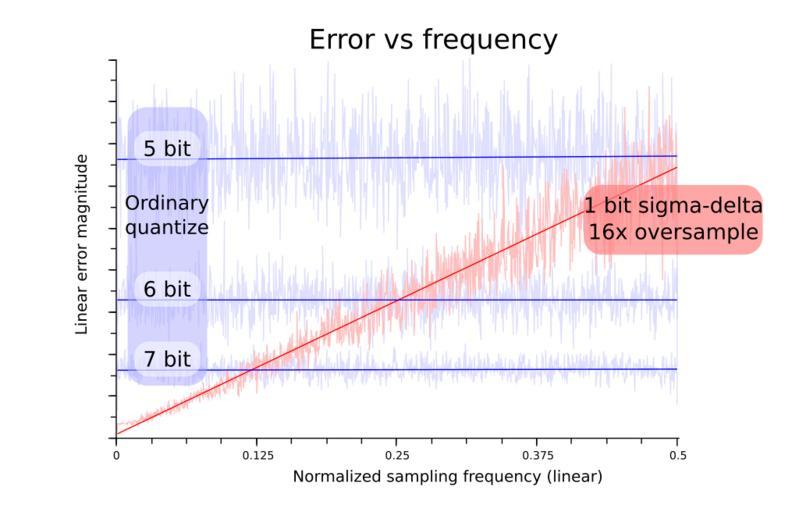
| Keywords: Delta sigma dithering 1st order err vs frq.svg en A graph of the quantization noise performance of a 64x oversampled 1-bit delta-sigma vs frequency up to 1/2 of the 1x sample rate from simulation Noise due to 5 6 7 bit ordinary quantization is also shown for comparison This file was created by running the scilab script listed below many times about 20 to average the results The lines are least-squares best fit while the lighter randomness is the actual data own Darrell barrell 2008-06 SCILAB script <pre><nowiki> //-------------------------------------------------------------------------------------- // Investigate equivalent bit resolution of first-order delta-sigma dithered // quantized samples for various oversampling amounts using random data oversampling // and applying the following delta-sigma dithering // // outn quantize inn+errsumn // errsumn+1 errsumn + inn - outn // // The output is then perfectly filtered decimated back to the original sample rate // and the standard deviation of the error difference between input output is found // // The number of bits resolution at the original sample rate giving the same error is // then calculated // // e g if we oversample 4 bits by 8 times using delta-sigma dithering and then perfectly // filter the output what is the equivalent bit resolution at the original sample rate // // Notes // perfectly filtering means using the FFT and zeroing unwanted bins // // Input data is not quite uniform distribution because of oversampling and then // normalizing to ensure no out of range data // // Calaculation of effective bit resolution assumes evenly distributed input data // which isn't exactly the case as stated in the above note // // This script is public domain // // version 1 June 2008 darrell barrell // //-------------------------------------------------------------------------------------- function out real_fft x // real to complex fft real length must be divisible by 4 out fft x ; out out 1 ; out 2 /2 2; out /2+1 ; endfunction //-------------------------------------------------------------------------------------- function out real_ifft x // complex to real fft real length must be divisible by 4 t x 1 ; x 2 -1 5; x ; conj x -1 -1 2 5; out real ifft t ; endfunction //-------------------------------------------------------------------------------------- function out clip x lower upper // clip x to be within bounds lower and upper out max min x upper lower ; endfunction //-------------------------------------------------------------------------------------- function n_bits equiv_bits stdev_quan_err // // find the equivalent number of sampling bits resolution that gives a quantizing // error std deviation of stdev_quan_err // // Assume // linear quantizing // rounding to closest quantized value // uniform input distribution // full scale conversion i e quantized output is from 0 to 1 // // stdev_quan_err sqrt 1/12 / 2 quan_bits-1 ; // // Note sqrt 1/12 is the stdev of uniform distribution with // an output range of 1 unit // n_bits log 1 / sqrt 12 stdev_quan_err + 1 / log 2 ; endfunction //-------------------------------------------------------------------------------------- function lsq_line_plot dat col_rgb // plot dat and also least-squares best fit line in colour col_rgb plot dat foreground col_rgb 25+ 75 ; len length dat ; A lsq 1 len ' ones len 1 dat ; plot 1 len A 2 +A 1 1 len foreground col_rgb ; endfunction //-------------------------------------------------------------------------------------- function frq_err sum_frq_err_sqr frq_err err // get the freq error squared of err err real_fft err ; frq_err frq_err + real err 2 + imag err 2; endfunction //-------------------------------------------------------------------------------------- // resample factor oversample_v 2 4 8 16 32 64; oversample_v 16; //oversample_v 8; // data length len_d 2048; // dithered bit resolutions to test dith_bits_v 1 4 8 12; dith_bits_v 1; // ordinary quantized bit resolutions to plot quan_bits_v 1 16; // create some random data d rand len_d 1 ; // maximum oversample max_over max oversample_v ; // use FFT resample fft_d real_fft d ; // pad spectrum with 0 fft_d length d /2 max_over+1 0; // resampled data at maximum resample rate d_max_resamp real_ifft fft_d max_over; // normalize resampled data between 0 1 // note that the distribution is no longer uniform min_r min d_max_resamp ; max_r max d_max_resamp ; d_max_resamp d_max_resamp-min_r / max_r-min_r ; d d-min_r / max_r-min_r ; //printf resample error f\n sum d_max_resamp 1 max_over -d 2 ; // do ordinary quantizing to test quan_err ; for n 2 quan_bits_v-1 d_quan round d n /n; quan_err +1 stdev d_quan - d ; end equiv_bits quan_err scf 1 ; title Quantizing performance of 1st order sigma-delta dithering ; xlabel Times oversample ; ylabel Equivalent bit resolution ; xgrid; // dithered bit resolution for bits dith_bits_v // number of quantizing levels levels 2 bits-1; // oversampling over 2; // std deviation of dithering error after perfect resample dith_err ; for over oversample_v printf levels d over d\n levels over ; // decimate resampled data to get resampling that we want decimate_stp max_over/over; d_resamp d_max_resamp 1 decimate_stp ; // current error sum err 0; // do the dithering to dith zeros len_d over 1 ; for idx 1 length d_resamp // input sample in d_resamp idx ; // output sample gets first order sigma-delta dithered rounded out round in+err levels /levels; out clip out 0 1 ; // update error err err + in - out; // output dith idx out; end // perfect filter decimate using FFT dith_fft real_fft dith /over; dith_dec real_ifft dith_fft 1 len_d/2+1 ; // noise power due to quantizing errors in dB using the // standard deviation which is sqrt power dith_err +1 stdev d-dith_dec ; end dith_equiv_bits equiv_bits dith_err ; plot dith_equiv_bits ; plot dith_equiv_bits 'x' ; if length dith_equiv_bits > 1 printf f diff dith_equiv_bits ; printf \n ; end end // initialize frq error sums if ~ exists frq_err_dith frq_err_dith 0; frq_err_qa 0; frq_err_qb 0; frq_err_qc 0; end // frq_err_dith sum_frq_err_sqr frq_err_dith d-dith_dec ; // compare with ordinary quantizing at the closest bit depths -1 0 +1 t 2 round dith_equiv_bits ; frq_err_qa sum_frq_err_sqr frq_err_qa d-round d t 2-1 / t 2-1 ; frq_err_qb sum_frq_err_sqr frq_err_qb d-round d t-1 / t-1 ; frq_err_qc sum_frq_err_sqr frq_err_qc d-round d t/2-1 / t/2-1 ; scf 2 ; clf; title Comparison of error vs frequency ; xlabel Frequency linear ; ylabel Error magnitude linear ; lsq_line_plot sqrt frq_err_qc 0 0 1 ; lsq_line_plot sqrt frq_err_qb 0 0 1 ; lsq_line_plot sqrt frq_err_qa 0 0 1 ; lsq_line_plot sqrt frq_err_dith 1 0 0 ; printf Done\n ; </nowiki></pre> Digital signal processing | ||||