MAKE A MEME
View Large Image
| View Original: | Effect of circular convolution on discrete Hilbert transform.png (1156x608) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
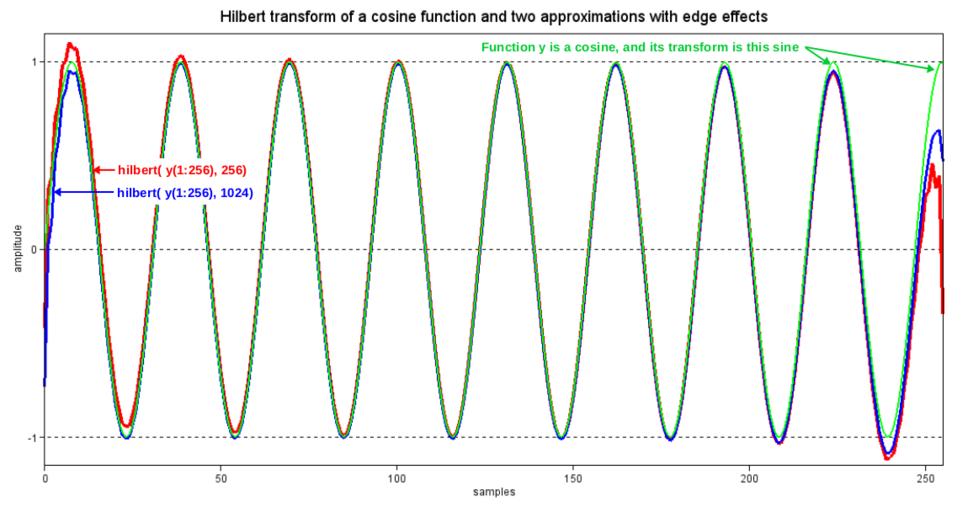
| Keywords: Effect of circular convolution on discrete Hilbert transform.png Hilbert transform of cos ωt is sin ωt When a finite segment of cos ωt is transformed edge effects inevitably occur Using a segment length of 256 samples this figure shows a sine function and two approximate Hilbert transforms computed by the MATLAB library function hilbert · which supports optional zero-filling of the segment to be transformed The red graph is the result of no zero-filling and the blue graph is the result of 300 zero-filling In the latter case the edge effects are almost all due to the rise and fall times of the Hilbert transform's 2/ Ď n impulse response In the red case we have the added effect of circular convolution In other words in the blue case distortion occurs when some of the filter taps are coinciding with zeros instead of with samples of cos ωt And in the red case those same taps are coinciding with wrapped-around and out-of-phase samples of cos ωt 2012-09-13 18 40 32 own Bob K Scilab commands <source lang Scilab > N 256; x 0 N-1; cycles_per_segment 8 2888; // empirical value that displays edge effects well cycles_per_sample cycles_per_segment/N; Yreal cos 2 pi cycles_per_sample x ; // function to be transformed Ans sin 2 pi cycles_per_sample x ; // the ideal answer H1 imag hilbert Yreal ; // no zero-filling H2 imag hilbert Yreal zeros 1 1024-N ; // zero-filling // Display the results red 5; blue 2; green 3; black 1; // based on a call to getcolor top green; middle blue; bottom red; plot2d x' H1' H2 1 N ' Ans' style bottom middle top rect 0 -1 15 N-1 1 15 ; a gca ; a box on ; a font_size 2; //set the tics label font size a visible on ; a grid -1 0; a auto_ticks off off off a y_ticks tlist ticks locations labels -1 0 1 -1 0 1 ; a x_ticks tlist ticks locations labels 0 50 100 150 200 250 0 50 100 150 200 250 ; //a children children thickness 2; // set line thickness of plots top 1; middle 2; bottom 3; a children children top thickness 2; a children children middle thickness 3; a children children bottom thickness 4; xlabel samples fontsize 2 ylabel amplitude fontsize 2 title Hilbert transform of a cosine function and two approximations with edge effects fontsize 4 </source> cc-zero See also thumb left Discrete Hilbert transforms of a cosine function using piecewise convolution Signal processing Convolution | ||||