MAKE A MEME
View Large Image
| View Original: | Eigenvectors.gif (300x300) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
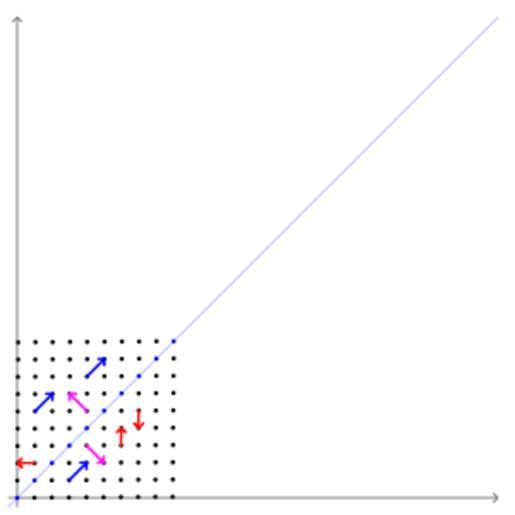
| Keywords: Eigenvectors.gif The transformation matrix <math>\bigl \begin smallmatrix 2 1\\ 1 2 \end smallmatrix \bigr</math> preserves the direction of vectors parallel to <math>\bigl \begin smallmatrix 1 \\ 1 \end smallmatrix \bigr </math> in blue and <math>\bigl \begin smallmatrix 1 \\ -1 \end smallmatrix \bigr </math> in violet The points that lie on the line through the origin parallel to an eigenvector remain on the line after the transformation The vectors in red are not eigenvectors therefore their direction is altered by the transformation Notice that the blue vectors are scaled by a factor of 3 This is their associated eigenvalue The violet vectors are not scaled so their eigenvalue is 1 own 2012-05-15 Kieff Extended version showing all quadrants left 300px Eigenvalue problems Affine transformation Animations of geometry | ||||