MAKE A MEME
View Large Image
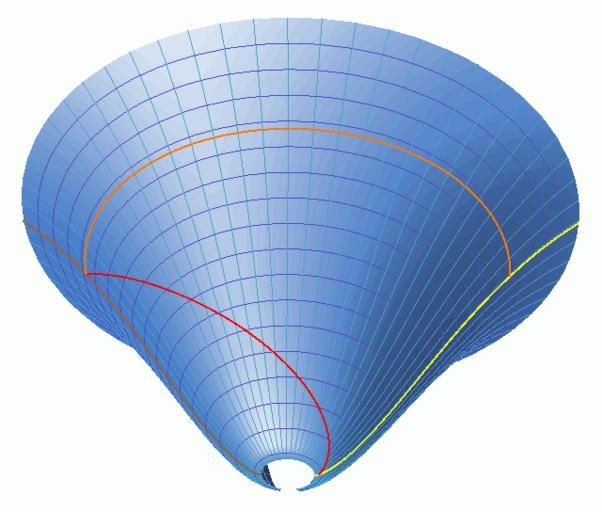
| View Original: | Embedded LambdaCDM geometry.png (640x544) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Embedded LambdaCDM geometry.png Euclidean embedding of a part of the Lambda-CDM spacetime geometry showing the Milky Way brown a quasar at redshift z 6 4 yellow light from the quasar reaching the Earth after approximately 12 billion years red and the present-era metric distance to the quasar of approximately 28 billion light years orange Lines of latitude purple are lines of constant cosmological time spaced by 1 billion years; lines of longitude cyan are world lines of objects moving with the Hubble flow spaced by 1 billion light years in the present era less in the past and more in the future Own work see mathematical details below 2008-03-18 Ben Rudiak-Gould Public domain an attribution would be appreciated but isn't required Image Embedded LambdaCDM geometry alt view png Mathematical details The FLRW metric with two spatial dimensions suppressed is <math>ds 2 c 2 dt 2 - a t 2 dx 2</math> where <math>a t_ \text now 1</math> If we flip the sign of the dx term making the metric Euclidean it can be embedded isometrically in Euclidean 3-space with cylindrical coordinates <math> r \phi z </math> by <math>\begin align r a t R \\ \phi x / R \\ z \int \sqrt c 2 - a' t 2 R 2 \ dt \end align </math> where R is a free parameter z is only defined when <math> a' t \le c/R</math> and <math>a' t </math> goes to infinity for both small and large t in ΛCDM so a smaller R allows us to embed a larger fraction of the universe's history On the other hand with a large R we can embed larger spatial distances since the embedding curves around on itself at a comoving distance of 2Ï R Ignoring the effects of radiation in the early universe and assuming k 0 and w ˆ’1 the ΛCDM scale factor is <math>a t \left \frac \Omega_m \Omega_v \sinh 2 \left \frac32 \sqrt \Omega_v H_0 t \right \right \frac13 </math> and the WMAP five-year report gives <math>\begin align \Omega_m \approx 0 279 \\ \Omega_v \approx 0 721 \\ H_0 \approx 70 1\ \text km \ \text s -1 \ \text Mpc -1 \approx 0 0717\ \text Gyr -1 \end align </math> Mpc megaparsec Gyr gigayear For the embedding above I chose <math>R c / a' 0 7\ \text Gyr \approx 9\ \text Gly </math> and a time range of 0 7 Gyr to 18 Gyr I deliberately cut off the embedding short of a full circle to emphasize that space does not loop back on itself or if it does not at a distance governed by the arbitrary parameter R The path of the light ray satisfies <math>dx/dt c/a t </math> Check categories 2008 November 14 en wikipedia Metric_expansion_of_space General relativity Cosmology | ||||