MAKE A MEME
View Large Image
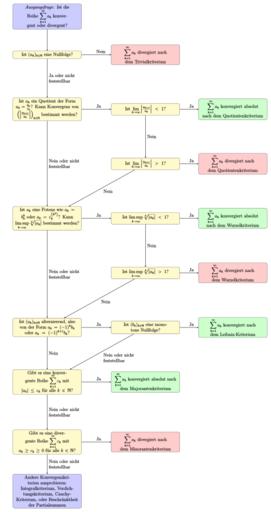
| View Original: | Entscheidungsbaum zur Konvergenz und Divergenz von Reihen.svg (825x1638) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Entscheidungsbaum zur Konvergenz und Divergenz von Reihen.svg de Entscheidungsbaum zur Konvergenz und Divergenz von Reihen 2016-10-22 own http //kulla me Stephan Kulla User Stephan Kulla other versions <gallery> Konvergenzschema für Reihen pdf Version von Benutzer Who2010 </gallery> Source code <syntaxhighlight lang tex> \documentclass12pt border 10pt standalone \usepackagelatin1 inputenc \usepackage amsmath \usepackage amssymb \usepackage tikz \usetikzlibrary shapes arrows positioning \everymath \displaystyle \newcommand \N \mathbb N \begin document \tikzstyle decision rectangle draw fill yellow 20 text centered rounded corners \tikzstyle label text width 3cm \tikzstyle block rectangle draw fill blue 20 text centered rounded corners \tikzstyle convergence rectangle draw fill green 20 node distance 8cm text centered rounded corners \tikzstyle divergence rectangle draw fill red 20 node distance 8cm text centered rounded corners \tikzstyle line -stealth thick draw \begin tikzpicture node distance 5cm auto text width 6cm \node block init \emph Ausgangsfrage Ist die Reihe \sum_ k 1 \infty a_k konvergent oder divergent ; \node decision below of init node distance 3 5cm questiontrivialkriterium Ist a_k _ k\in\N eine Nullfolge ; \node divergence right of questiontrivialkriterium node distance 9cm trivialkriterium \sum_ k 1 \infty a_k divergiert nach dem Trivialkriterium ; \node decision below of questiontrivialkriterium question_ratio_test Ist a_k ein Quotient der Form a_k \tfrac b_k c_k Kann Konvergenz von \left \left \tfrac a_ k+1 a_k \right \right _ k\in\N bestimmt werden ; \node decision right of question_ratio_test node distance 9cm rtcase1 Ist \lim_ k\to\infty \left \tfrac a_ k+1 a_k \right < 1 ; \node decision below of rtcase1 rtcase2 Ist \lim_ k\to\infty \left \tfrac a_ k+1 a_k \right > 1 ; \node convergence right of rtcase1 ratio_yes \sum_ k 1 \infty a_k konvergiert absolut nach dem Quotientenkriterium ; \node divergence right of rtcase2 ratio_no \sum_ k 1 \infty a_k divergiert nach dem Quotientenkriterium ; \node decision below of rtcase2 rootcase1 Ist \limsup_ k\to\infty \sqrtk a_k < 1 ; \node decision left of rootcase1 node distance 9cm question_root_test Ist a_k eine Potenz wie a_k b_k k oder a_k c_k \left k 2\right Kann \limsup_ k\to\infty \sqrtk a_k bestimmt werden ; \node decision below of rootcase1 rootcase2 Ist \limsup_ k\to\infty \sqrtk a_k > 1 ; \node convergence right of rootcase1 root_yes \sum_ k 1 \infty a_k konvergiert absolut nach dem Wurzelkriterium ; \node divergence right of rootcase2 root_no \sum_ k 1 \infty a_k divergiert nach dem Wurzelkriterium ; \node decision below of rootcase2 leibniz_case Ist b_k _ k\in\N eine monotone Nullfolge ; \node convergence right of leibniz_case leibniz_yes \sum_ k 1 \infty a_k konvergiert nach dem Leibniz-Kriterium ; \node decision left of leibniz_case node distance 9cm leibniz_question Ist a_k _ k\in\N alternierend also von der Form a_k -1 k b_k oder a_k -1 k+1 b_k ; \node decision below of leibniz_question majorcase Gibt es eine konvergente Reihe \sum_ k 1 \infty c_k mit a_k \le c_k für alle k\in\N ; \node decision below of majorcase node distance 5 5cm minorcase Gibt es eine divergente Reihe \sum_ k 1 \infty c_k mit a_k\ge c_k\ge 0 für alle k\in\N ; \node block below of minorcase node distance 4 5cm end Andere Konvergenzkriterien ausprobieren \\ Integralkriterium Verdichtungskriterium Cauchy-Kriterium oder Beschränktheit der Partialsummen ; \node convergence right of majorcase node distance 9cm major_yes \sum_ k 1 \infty a_k konvergiert absolut nach dem Majorantenkriterium ; \node divergence right of minorcase node distance 9cm minor_no \sum_ k 1 \infty a_k divergiert nach dem Minorantenkriterium ; \path line init edge questiontrivialkriterium ; \path line questiontrivialkriterium -- node xshift 3cm Nein trivialkriterium ; \path line questiontrivialkriterium -- node label Ja oder nicht feststellbar question_ratio_test ; \path line question_ratio_test -- node xshift 3cm Ja rtcase1 ; \path line rtcase1 -- node Nein rtcase2 ; \path line rootcase1 -- node Nein rootcase2 ; \path line question_ratio_test -- node label Nein oder nicht feststellbar question_root_test ; \path line rtcase2 -- node label Nein question_root_test ; \path line rtcase1 -- node xshift 3cm Ja ratio_yes ; \path line rtcase2 -- node xshift 3cm Ja ratio_no ; \path line rootcase1 -- node xshift 3cm Ja root_yes ; \path line rootcase2 -- node xshift 3cm Ja root_no ; \path line question_root_test -- node label Nein oder nicht feststellbar leibniz_question ; \path line rootcase2 -- node Nein leibniz_question ; \path line question_root_test -- node xshift 3cm Ja rootcase1 ; \path line leibniz_question -- node xshift 3cm Ja leibniz_case ; \path line leibniz_case -- node xshift 3cm Ja leibniz_yes ; \path line leibniz_question -- node label Nein majorcase ; \path line leibniz_case -- node label Nein oder nicht feststellbar majorcase ; \path line majorcase -- node label Nein oder nicht feststellbar minorcase ; \path line minorcase -- node label Nein oder nicht feststellbar end ; \path line majorcase -- node xshift 3cm Ja major_yes ; \path line minorcase -- node xshift 3cm Ja minor_no ; \end tikzpicture \end document </syntaxhighlight> cc-zero Series mathematics Decision diagrams Flow charts | ||||