MAKE A MEME
View Large Image
| View Original: | InfiniteSquareWellAnimation.gif (300x280) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
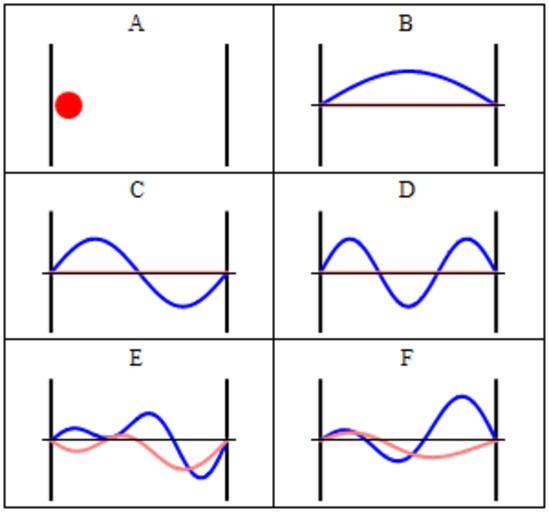
| Keywords: InfiniteSquareWellAnimation.gif en Trajectories of a particle in a box also called an infinite square well in classical mechanics A and quantum mechanics B-F In A the particle moves at constant velocity bouncing back and forth In B-F wavefunction solutions to the Time-Dependent Schrodinger Equation are shown for the same geometry and potential The horizontal axis is position the vertical axis is the real part blue or imaginary part red of the wavefunction B C D are stationary states energy eigenstates which come from solutions to the Time-Independent Schrodinger Equation E F are non-stationary states solutions to the Time-Dependent but not Time-Independent Schrodinger Equation Both E and F are randomly-generated superpositions of the four lowest-energy eigenstates B-D plus a fourth not shown own Sbyrnes321 2011-04-26 <pre> Source code written in Mathematica 6 0 by Steve Byrnes Apr 2011 This source code is public domain Shows classical and quantum trajectory animations for an infinite-square-well potential Assumes L hbar 1 m 2 pi -2 so that the nth energy eigenstate has energy n 2 ClearAll Global` Wavefunctions of the energy eigenstates psin_ x_ Sinn Pi x 2 1/2 ; energyn_ n 2; psitn_ x_ t_ psin x Exp-I energyn t; A random time-dependent state SeedRandom1; CoefList TableRandom Exp2 Pi I Random n 1 4 ; CoefList CoefList/NormCoefList; Randpsix_ t_ SumCoefListn psitn x t n 1 4 ; Another random time-dependent state SeedRandom2; CoefList2 TableRandom Exp2 Pi I Random n 1 3 ; CoefList2 CoefList2/NormCoefList2; Randpsi2x_ t_ SumCoefList2n psitn x t n 1 3 ; Set default style for plots SetOptionsPlot PlotRange -> - 05 1 05 -2 5 2 5 Ticks -> None PlotStyle -> DirectiveThick Blue DirectiveThick Pink Axes -> True False ; SetOptionsListPlot PlotRange -> - 05 1 05 -2 5 2 5 Axes -> False ; Draw walls walls ListPlot 0 -2 5 0 2 5 1 -2 5 1 2 5 Joined -> True PlotStyle -> Thick Black Thick Black ; Make the classical plot a red ball bounces back and forth classicaltrajectoryt_ left_ right_ 2 right - left Abst - Roundt + left; classicalballt_ left_ right_ ListPlot classicaltrajectoryt left right 0 PlotStyle -> DirectiveRed AbsolutePointSize15; classicalt_ label_ Showwalls classicalballt 1 9 PlotLabel -> label; Make the quantum plots plotpsin_ t_ label_ Showwalls Plot Repsitn x t Impsitn x t x 0 1 PlotLabel -> label Axes -> True False Ticks -> None; plotrandt_ label_ Showwalls Plot ReRandpsix t ImRandpsix t x 0 1 PlotLabel -> label Axes -> True False Ticks -> None; plotrand2t_ label_ Showwalls Plot ReRandpsi2x t ImRandpsi2x t x 0 1 PlotLabel -> label Axes -> True False Ticks -> None; Put all the plots together MakeFramet_ GraphicsGrid classical3 t/ 4 Pi A plotpsi1 t B plotpsi2 t C plotpsi3 t D plotrandt E plotrand2t F Frame -> All ImageSize -> 300; output TableMakeFramet t 0 4 Pi 138/139 4 Pi/139 ; SetDirectory C \\Users\\Steve\\Desktop Export test gif output DisplayDurations -> 10</pre> Cc-zero Animations of quantum wave functions 1D infinite square wells Images with Mathematica source code Animated GIF | ||||