MAKE A MEME
View Large Image
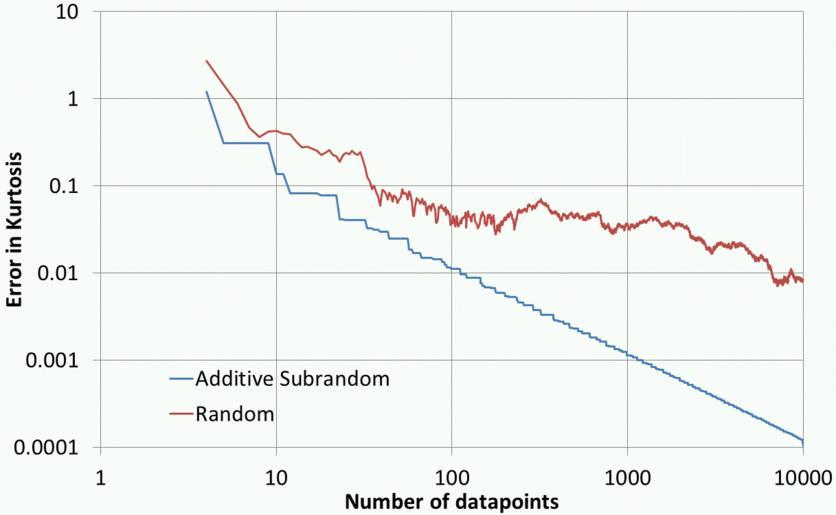
| View Original: | Subrandom Kurtosis.gif (1217x750) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Subrandom Kurtosis.gif en Error in estimated kurtosis as a function of number of datapoints 'Additive subrandom' gives the maximum error when c sqrt 5 -1 /2 'Random' gives the average error over six runs of random numbers where the average is taken to help smooth out fluctuations own Mollwollfumble 2011-04-05 Check categories 2011 April 6 en wikipedia Subrandom_numbers 2 Randomness Number theory | ||||