MAKE A MEME
View Large Image
| View Original: | Universal Resonance Curve.svg (100x100) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
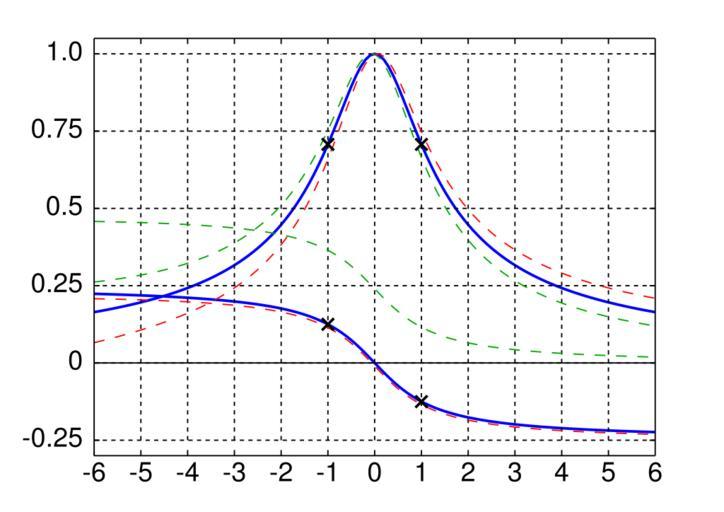
| Keywords: Universal Resonance Curve.svg en Frederick E Terman's Universal Resonance Curve a symmetric approximation to the normalized response of a resonant circuit; abscissa values are deviation from Fc in units of Fc/ 2Q the 3dB-half-bandwidth; ordinate is relative amplitude and phase in cycles The upper green dashed phase curve is from a system of two poles and no zero which lags 90 degrees 0 25 cycle at resonance The other red dashed curves are for a pair of poles with a zero at DC at s 0 in Laplace notation which is what is usually approximated by the universal resonance curve or was in Siebert; in terms of magnitude gain it is asymmetric in the opposite direction of the green curve These curves are calculated for a Q value of 4; higher Q values will give curves closer to the universal curve The X's represent deviations of one half-bandwidth plus or minus Fc/2Q the -3dB points gains of 0 707 and phase shifts of 45 degrees 0 125 cycle self made roughly about Siebert 1986 http //books google com/books id zBTUiIrb2WIC pg PA113 dq siebert+universal-resonance-curve ei qtjbSruNBInmkATFrqyeCA v onepage q f false Circuits Signals and Systems p 113 Richard F Lyon User Dicklyon 2009-10 Electronics Cauchy-Lorentz distributions Resonance dddddd | ||||